1. Greedy Algorithms and Least Cost Hamiltonians

Using the greedy strategy we obtain the following cycles and costs:

A-B-C-D-E-A: $27
B-A-C-D-E-B: $27
C-A-B-D-E-C: $27
D-A-B-C-E-D: $27
E-A-B-C-D-E: $27

Now if we take the following tour: A-D-C-E-B-A, the cost is $24. Even if we don't know if this new tour is the least cost Hamiltonian cycle, we can surely say that the greedy strategy is not optimal.

2. Hamiltonian Cycles in Dense Graphs

The algorithm goes as follows:

Connect the vertices arbitrarily in a Hamiltonian cycle H (O(n) time)
For every edge (v,w) in H not in the input graph G do: (there are at most n)
- remove the edge (v,w) from H. (O(1) time)
- Let v, x₁, x₂, x₃, ..., x_n-2, w be the resulting Hamiltonian path. Find the pair (x_i,x_i+1) in this path such that v is connected to x_i+1 and w is connected to x_i in 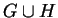$G \cup H$ . Note that (v,w) has been removed from H. (O(n) time it's a simpe scan of the path)
- The resulting new Hamiltonian cycle H is v, x_i+1, x_i+2,..., w, x_i, x_i-1, ..., v. Note that we have removed 2 edges (v,w) and (x_i,x_i+1) and added 2, (v,x_i+1)) and (x_i,w).
stop when all edges not in the input graph G have been removed.

The data structures used here are a simple linked list for the hamiltonian circuit and a adjacency matrix for the graph. Why the adjacency matrix and not an adjacency list (usually better and more flexible)?

Because we want to be able to check fast if an edge belong to the graph and that can be done in O(1) time with the matrix whereas it could take as much as O(n) time in the adjacency list especially for dense graphs.

The time complexity is O(n²). Replacing one edge is O(n) time. There are at most n edges to replace hence the O(n²) complexity.

3. Prim's Minimum Spanning Tree Algorithm for Graphs

Recall the main idea behind Prim's algorithm. Assume we already have a subset of the MST, we grow the tree by finding the minimum-cost edge connecting the MST to the vertices not already in the MST.

The input is Weight[i,j] the weight matrix. The output is MST[i,j] the Minimum Spanning tree.

We will need two extra arrays of size n to solve the problem in O(n²). The first array defines the closest point to each vertex. Let's call this array Nearest. We have Nearest[i]=j, means that j is the closest vertex to i. The second array is used to store the distance from i to it closest vertex j, thus Distance[i]=Weight[i,j]. The algorithm goes as follows:

1. For every vertex V_i, initialize Nearest[V_i] to a dummy node and Distance[V_i] to 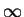$\infty$ . let V_new be the last vertex added in the MST. We initialize V_new=1 the first vertex of our graph.
2. For every vertex $V_i \neq V_{new}$ , if Weight[V_new,V_i]<Distance[V_i] update Nearest[V_i] and Distance[V_i]. (one scan of the row corresponding to vertex V_new in Weight, thus linear time)
3. Find the minimum distance in Distance. Output the index k (scan the array once, thus linear time).
4. add the edge (k,Nearest[k]) in the MST matrix (constant time).
5. let V_new=k
6. Go back to step 2 until all vertices have been added to the MST (we have n vertices so the algorithm loops n times).

Step 2 of the algorithm ensure that we always have the closest neighbors of the vertices already in the MST, stored in Nearest and their corresponding weights in Distance. Step 3 will find the smallest such distance, thus obtaining the new edge to add in the MST.

The Step 2 and 3 are O(n), step 4 and 5 are constant. Those 4 steps are repeated n times thus an O(n²) time complexity.

Sylvain Bouix
2000-12-16