1. Substractions using a Turing Machine
Here is a solution with only 5 states. It's pretty clever so
I encourage you to try it out with a few examples. Here it is:
Assume x is the first number, and y the second we
want x-y.
| Current State | Current Symbol | Action | New State | Why? |
| 1 | X | R | 1 | go to the rightmost digit of x |
| 1 | - | R | 2 | end of x has been read; Right, state 2 |
| 2 | X | L | 3 | sees the leftmost digit of y; Left, state 3 |
| 3 | - | L | 3 | looks for the rightmost digit of x |
| 3 | X | - | 4 | erases it; state 4 |
| 4 | - | R | 4 | goes right looking for the leftmost digit of y |
| 4 | X | - | 1 | erases it (it's been erased in x by state 3); Loop back to state 1 |
| 2 | - | L | 0 | no digit left in y; stop state 0 |
| 0 | STOP | Done! |
The best way to understand the algorithm is to try a simple example. I recommend you to work it out for XXX-XX
2. Growth of Functions
Here is the graph that you should have obtained.MATLAB is the software I used to create this plot.
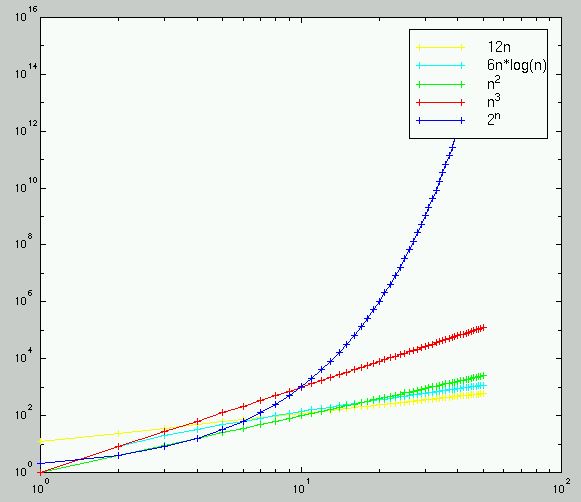
3. Big "Oh" Notation
a. 100n+log n = O(n+(log n)^2)
Proof:
100n = O(n) and log(n) = O((log n)^2))
By lemma 3.2 100n+log n = O(n+(log n)^2).
b. log n = Theta(log(n^2))
Proof: log(n^2) = 2 log(n) = Theta(log(n))
c. (n^2)/(log(n)) = Omega(n*(log(n))^2)
Proof:
Multiply both by n.log(n) gives n and (log n)^3.
Using the definition of big Oh, we need to find some constant
c and a number n_0 so that
for the relation n^2 >= c.log(n)^3 holds for any n >= n_0
Take c = 1 and n_0 = 8
d. (log n)^(log n) = Omega(n/log(n))
Multiply by log(n) gives (log n)^((log n)+1)
Using the definition of big Oh, we need to find some constant
c and a number n_0 so that
for the relation (log n)^(log n + 1)>= c.n holds for any n
>= n_0
Take c = 1 and n_0 = 8
e. n^0.5 = Omega ((log n)^5)
Proof:
Using the definition of big Oh, we need to find some constant
c and a number n_0 so that
for the relation n^0.5 >= c.(log n)^5 holds for any n >=
n_0
Take c = 1 and n_0 = 100
f. n*2^n = O(3^n)
Proof:
Using the definition of big Oh, we need to find some constant
c and a number n_0 so that
for the relation n.2^n <= c.3^n holds for any n >= n_0
Take c = 1 and n_0 = 10
Extra question (we discussed this during the tutorial):
Show: n/2 log(n/2) = Omega(n log n)
Proof:
First multiply both sides by 2/n. We get log(n/2) and (2 log n).
Using the definition of big Oh, we need to find some constant
c and a number n_0 so that
for the relation log(n/2) >= c.2 log n holds for any n >=
n_0
Now, log(n/2) >= c.2 log n
==> log n -log 2 >= 2.c.log n
==> (1 - 2c) log n >= 1
For c = 1/10 and n_0 = 3, this relation holds for any n >=
3
4. Minimum Spanning Trees
Far the easiest way to prove this question is by contradiction. The proof by contradiction here goes as follows.
Remember that in any proof by contradiction, we assume the negation of the claim, and show that this negation leads inevitably to a contradiction. Here the claim C is that, for any set of points S (some red, some blue), the closest pair of opposite-colored points are connected by an edge in the MST of S. The negation of this claim, not(C), is that for some set of points S, the closest pair of opposite-colored points are {\em not} connected by an edge in the MST of S. This is what we want to show leads to contradiction.
Suppose not(C) is true. Call the closest pair of opposite-colored points in S b_1 and r_1 (blue and red, respectively). So, by not(C), the MST of S does not have an edge between b_1 and r_1. However, since the MST is a spanning tree, it must contain some path from b_1 to r_1.
Consider this path.
Since it starts at a blue point (b_1)
and ends at a red point (r_1), the path
must contain at least one edge joining a blue point to a red point.
Call the points joined by this edge b_2
and r_2. (Note that it's possible that
b_2 = b_1
or r_2 = r_1,
but not both, since we know that b_1
and r_1 are not connected by an edge
in the graph.)
Now, suppose we insert edge (b_1 r_1) into the MST. This will form a cycle, since there are now two paths from b_1 to r_1.
Next, remove edge (b_2 r_2). The resulting graph is still a spanning tree, because every two points which were previously connected by a path through (b_2 r_2) are now connected by a path through (b_1 r_1).
But what has happened to the graph's total edge length? We've inserted an edge between the closest red-blue pair, and removed an edge between some other red-blue pair. So the edge removed was longer than the edge inserted. (We ignore here the case where there's a tie for the closest red-blue pair, but that case isn't hard to deal with.) Therefore the total edge length must have decreased. But this contradicts our assumption that the previous graph was the MST (minimal spanning tree). Thus, not(C) has led to contradiction, and therefore C must be true.