CS360: Answers to Assignment 4
Answers to Assignment 4
Question 1:
Marked by Erin (mcleish@cs.mcgill.ca)
(A) Give a direct reduction from Independent set to Vertex Cover:
Independent Set
Instance: A Graph G = (V,E) and an integer k
Question:Is there an independent set of size at least k in G?
Vertex Cover
Instance: A graph G = (V,E) and an integer k
Question: Is there a vertex cover of size at most k in G?
The reduction:
Suppose we are given an instance I to the independent set problem, consisting of a graph G and an integer k.
The instance to the Vertex Cover problem is simply:
-The same graph G=(V,E)
-the integer |V|-k
Proof of the reduction:
-
"yes"->"yes"
Suppose that (G,k) was a "yes" instance to the independent set problem. In other words, there IS an independent set
of size k in the graph G. Let S be those vertices in the independent set. And let C = V-S. Now consider the edges
of the graph G. For any edge e in E, it must be that one of its endpoints is in C. If this were not true, then both
of its endpoints would have been in the independent set, which is impossible. Therefore, C is a vertex cover of G, and
also C has size |V|-k. Therefore, the instance (G,|V|-k) is a "yes" instance to the Vertex cover problem.
- "no"->"no"
Suppose that (G,|V|-k) was a "yes" instance to the vertex cover problem. In other words, there IS a vertex cover of
size |V|-k in the graph G. Let C be those vertices in the vertex cover, and let S = V-C. Now consider the vertices in S.
Let v1 and v2 be any two vertices in S. Is it possible that there is an edge between v1
and v2? If this were true, then that edge would NOT have an endpoint in C. And this would mean that C was
not a vertex cover of G. Therefore, it is impossible that any two vertices in S are neighbours. Therefore S forms an
independent set, and it has size k. So a "no" to independent set maps to a "no" instance of vertex cover.
(B) Show that there is a polynomial time algorithm to find the maximum independent set in a bipartite graph.
The idea here is that we already know how to find the maximum matching in a bipartite graph. From the maximum matching, we
can get the minimum vertex cover, and then from the vertex cover, we can get the independent set by part (a). The details
below are far more than I expected on the assignment but they are good to review for the exam.
Here is
the algorithm:
Finding the Maximum matching:
-
Convert the Bipartite graph into a network flow
- Use Ford-Fulkerson to find the maximum flow.
- Each edge in the graph which has a positive flow, is now an edge in the maximum matching of G. This was actually done on your
assignment 3 and is shown in the text book.
- Let the set of edges in this matching be called M.
Finding the Minimum Vertex Cover
- Suppose that M is a perfect matching, (ie: no vertices are missing). If the graph partition is (A,B), then
the vertex cover is simply the vertices on side of the partition, which ever is smallest. In other words, the cover is
the min of A or B.
- Otherwise, M is not a perfect matching. An example is shown below where the matched edges are in red.
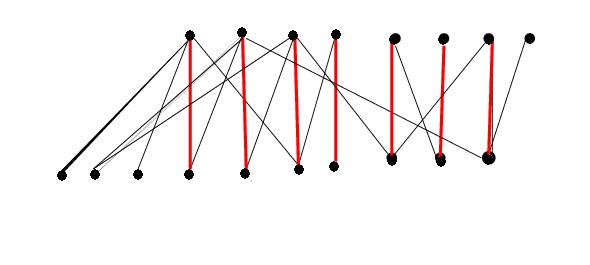
Let A be one side of the partition that has some vertices which are unmatched.
Let the unmatched vertices in A be labelled S. Let U be the set of vertices in A which are reachable from S by
alternating paths. And let T be the neighbours of U along edges in M. (See the figure below).
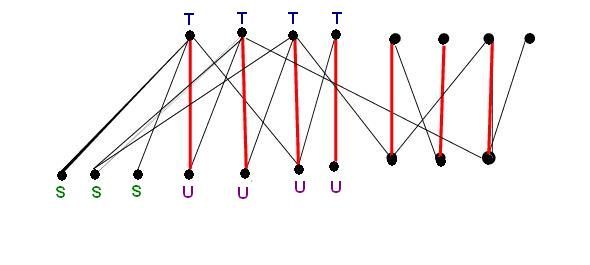
- The vertex cover is now (A-S-U)union(T). The size of this vertex cover is exactly the size of M. This is
because for each edge in the matching which touches a T vertex, we have exactly one vertex in the cover. Also, for
each each in the matching which does NOT touch a T vertex, we have exactly one vertex in the cover in the set (A-S-U). The
vertex cover is shown by the yellow vertices in the figure below:
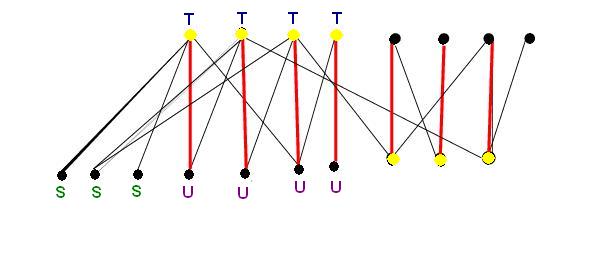
Finding the maximum independent set:
- This is easy, just take the vertices which are NOT in the vertex cover. This set is shown in green below.
Notice that none of the green vertices are neighbours.

The entire algorithm is polynomial. The Ford-Fulkerson algorithm is polynomial. After that, finding
the vertex cover is polynomial, since all we are doing is tracing alternating paths. Finally, taking the opposite
vertices to get the independent set is also polynomial.
Question 2:
Marked by Mark (jmerce1@cs.mcgill.ca)
Partition: Instance: Non-negative integers
A = {a1, a2, ..., an}
Question: Can the integers be split into two subsets of equal weight?
Show Partition is NP-complete.
Proof.
First we show that PARTITION is in NP. Our certificate will be a
subset S of A. We can verify in polynomial
time whether S and (A-S) have equal sums
(simply by taking the sum of the elements in S
and in (A-S)). If these sets have equal sums, then we accept.
Now we show that Partition is NP-complete via a reduction from
SUBSET-SUM (defined as: is there a subset of sum k in A?).
Let (A,k) be an
arbitrary instantance of SUBSET-SUM. We transform this into an instance A'
of the PARTITION problem in this way:
- Let m = (the sum of the elements in A).
- Let A' be the set A plus two more elements:
- an+1 = (2m+k), and
- an+2 = (3m-k).
A'
can be constructed easily in polynomial time.
I claim that A' is a true instance of PARTITION
iff (A,k) is a true
instance of SUBSET-SUM. Assume (A,k) is a true instance of
SUBSET-SUM. Then there is a subset S of A such that S
has size k.
Then ((A-S) union {an+1}, S union {an+2}) is a
PARTITION of A'.
Now assume that A' is a true instance of PARTITION. Then there exists an
equal-weight partition (S1, S2) of A'. Notice that
the sum of all the elements in A' is 6m. So both an+1
and an+2 cannot appear in the same subset. Without loss of
generality, we say that an+1 is in S1 and
an+2 is in S2. Then by construction
S2 - {an+2} has sum k (since S2 has
weight 3m). It follows that there is a subset of weight k in A.
Therefore,
The given reduction reduces SUBSET-SUM to PARTITION, and since SUBSET-SUM
is NP-complete, it follows that PARTITION is NP-hard. We have shown that
PARTITION is in NP, so PARTITION is NP-complete.
Question 3:
Marked by Mark (jmerce1@cs.mcgill.ca)
4-SAT is similar to 3-SAT, except that each clause contains exactly 4
distinct literals. Show that 4-SAT is NP-Complete.
Proof.
First we show that 4-SAT is in NP. 4-SAT is just a special case of
SAT (i.e. we can use the same certificate for 4-SAT as for SAT), and SAT
is in NP, thus 4-SAT is in NP.
Next we show that 4-SAT is NP-complete, by reducing 3-SAT to 4-SAT. Let
phi =
{C1, C2, ..., Cn}}
be an arbitrary instance of 3-SAT. Our
reduction will go like this. The set of variables in the new instance
will be the set of variables in phi, plus one new variable x.
To each Ci we add a new
literal x. We
also add a new clause
Cn+1 =
{not x, not x, not x, not x}. Call
this new instance phi'. This construction can be easily computed in
polynomial time.
We claim that phi' is in 4-SAT iff phi is in 3-SAT.
Assume phi' is in
4-SAT. Then Cn+1 must be satisfied.
Therefore x must be assigned
to false, therefore the fourth literal of each clause in phi' must be
false. Therefore there must be an assignment to the remaining variables
such that for each clause Ci, at least one of the
first three literals
is satisfied. It is easy to see that this is only possible if the original
3-SAT instance phi' is satisfiable. Now assume that the 3-SAT instance phi
is satisfiable by some assignment. Then we can satisfify phi' by
using the
satisfying assignment to phi and by setting x to false. Thus
phi' is in
4-SAT iff phi is in 3-SAT, and the claim is proven.
Question 4:
Marked by Marina (mtakan1@cs.mcgill.ca)
| Yummy | Juicy | Supply |
| fat | 1kg | 2kg | 60kg |
| sawdust | 2kg | 1kg | 48kg |
| Profits | $3 | $2 | |
(a)
Let x=number of units of Yummy, y=number of units of Juicy.
The problem can be formulated as an LP as follows:
maximize 3x+2y
subject to
| | x+2y<=60 |
| | 2x+y<=48 |
| | x>=0, y>=0 |
The feasible region is:
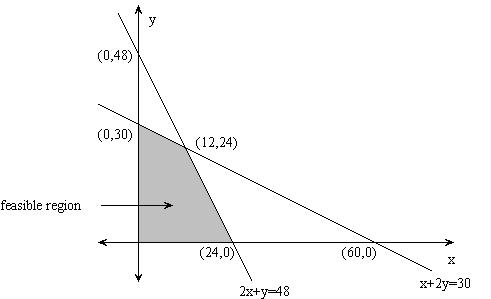
The point of intersection is (12,24).
Evaluate the objective function at the corners.
(24,0) : 3(24)+2(0)=72
(0,30) : 3(0)+2(30)=60
(12,24): 3(12)+2(24)=84
The maximum occurs at the point (12,24), ie. profit is optimum at $84 when 12 units of Yummy and 24 units of Juicy are produced.
(b)
The dual of the above problem is
minimize 60u+48v
subject to
| | u+2v>=3 |
| | 2u+v>=2 |
| | u>=0, v>=0 |
The feasible region is:
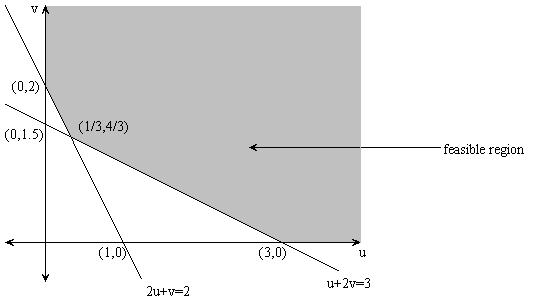
The point of intersection is (1/3,4/3).
Evaluate the objective function at the corners.
(3,0) : 60(3)+48(0)=180
(0,2) : 60(0)+48(2)=92
(1/3,4/3): 60(1/3)+48(4/3)=20+64=84
The minimum (optimum value) of 84 occurs at (1/3,4/3).
This gives a certificate of optimality, since the optimal values of the primal and dual LP are equal (strong duality theorem).

