308-360 Tutorial #7
ATTENTION: Please read this!!!! The tutorial (at least mine) was confusing (and I confused). This clears everything up - specifically please read the detailed solution to question 3 by Marina.
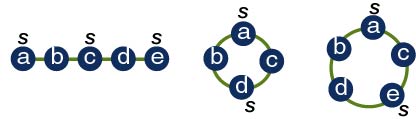
1. Derive an efficient algorithm for finding the largest independent set in a graph in which no vertex has degree more than two.
There are 4 types of graphs that have all degrees at most 2. The
algorithm is very straightforward, so write one up on your own.
Lone Vertex (degree 0)
If G is a graph of 1 vertex v, the stable set S = v.
Edge (all degree 1)
If G is an edge (u,v) then S = u or S = v.
Path (degree at most 2)
If G is a path then starting at one of the
1-degree vertices v, add v to S then alternate along the path leaving a
vertex out of S and then adding the vertex to S.
Cycle (all degree 2)
If G is a cycle, start at an arbitrary vertex and
alternate in choosing valid vertices for S along the cycle.

1 EXTRA. Derive an efficient algorithm for finding the largest independent set in a BIPARTITE graph.
Vertex Cover and Independent Set
V' is a minimum vertex cover of G=(V,E) if and only if V-V' is a
maximum independent set of G. The proof of this is in Lecture 16's notes. It
is simple to see why this is true. A vertex cover V' of G covers all the
edges in G. So the graph of V-V' has no edges and therefore V-V' is an
independent set.
Maximum Matching and Vertex Cover
The maximum cardinality of a matching M in G is equal to the minimum
cardinality of a vertex cover V'. (Konig)
Proof that |M| <= |V'|. Let M be any maximal matching of G. By definition,
all the endpoints of the edges in M are distinct. A cover of all the edges
in M would require at least one endpoint for each edge in M. So the M-cover
requires at least |M| vertices. The vertex cover of G, V' must consist of
the M-cover. So |V'| >= |M|.
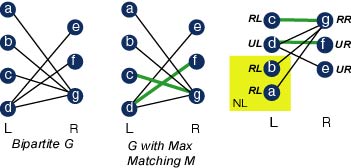
Proof that |V'| <= |M|. Let G be a bipartite graph with partitions
V = L U R. Let M be a maximum matching of G. To build V', we must
partition L and R into two sets each, the reachable set and the unreachable set.
Let NL be the set of non-matched vertices in L. Vertex v is in NL iff v in L andthere does not exist an edge with v as an endpoint in the matching M.
An M-alternating path is a path of edges that alternate being in M and not being in M. Use the concept of M-alternation path and the vertices in NL to
partition L and R into Reachable Left (RL), Unreachable Left(UL), Reachable
Right (RR) and Unreachable Right (UR). A vertex v is reachable iff it can be
visited by following an M-alternating path beginning at some vertex u in NL.
Note that any vertex in NL is in RL.
The proof finishes by showing that V' is in fact a vertex cover and that |V'| <= |M|. I am not going to prove this, you can easily convince yourself or look up a proof on the web. Simply put, V' = UL + RR and IS = V - V' = RL + UR.
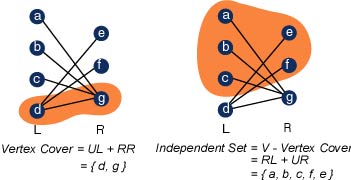
We know how to find a maximum matching of a bipartite graph using the max flow algorithm (FordF) in polynomial time. We can also determine the RL, UL, RR and UR sets in polynomial time. So we can determine the vertex cover and thus the independent set in polynomial time.
2. Bipartite matching is described in the tutorial 7 question sheet. The question is can you set up a polynomial time reduction from BIPARTITE MATCHING to integer valued flows (on a graph). I want you to write it out in the format of the reduction proofs we have seen for NP-complete problems.
Proof from Miguel Jette.
Let L and R be the two sets of vertices as we know them in the bipartite
graph. Then we have a new graph G', such that we add the vertex s such
that (s,u) is in G' for all u in L and c(s,u) = 1. Also we add the vertex
t such that (v,t) is in G' for all v in R and c(v,t) = 1. So that is just
like we said so far. Now like I said at the beggining of the class, the
old (u,v) with u in L and v in R have c(u,v) equal to infinity (doesn't
really matter.) [Given by Prof. Avis]
The capacities are right because as soon as we choosed (s,u) , u in L,
there is no way to choose u another time and thus we have a an edge
disjoint path from the other paths s to t. But if we assume the Ford
Fulkerson works well, then we know we have a max flow from s to t meaning
we have a Maximum Match between the u's in L and the v's in R.
PROOF:
Let us assume that we don't have a maximum match between u's and
v's. Therefore there is a way we can match u's and v's which will yield
to a better flow and will contradict our assumption that Ford Fulkerson
works... Therefore, we know the matching is maximum.
3. INDEPENDENT SET is NP-complete for graphs which have degree at most three. Use this to prove that CLIQUE is hard for graphs where every vertex is adjacent to at least one half of the other vertices. (Hint: what is the relationship between cliques in a graph and independent sets in the complement of the graph? What is the relationship between the degrees of vertices in a graph and their degrees in the complement?)
INDEPENDENT SET (IS)
Input: G = (V,E), deg(v)<=3 for all v in V. Integer k.
Question: Does there exist an independent set of size greater than k in
G, i.e. a subset V' of V, |V'| >= k, such that {u,v} is not an edge for all
u,v in V'.
CLIQUE[V/2] (CL[V/2])
Input: G = (V,E), deg(v) >= |V|/2 for all v in V. Integer k.
Question: Does there exist a clique of size greater than k in G,
i.e. a subset V' of V, |V'| >= k, such that {u,v} is an edge for all u,v
in V'.
First we reiterate the reduction from IS to CLIQUE given in class:
For a given instance of IS, G=(V,E), k:
Take G^, the complement of G.
Complement
G^ = (V,E^), E^ = (V x V)\(E U S) where S is the set of self
loops (S is the set of edges {u,u} for all vertices u in V), i.e. the
complement of G has the same vertices as G, but has exactly those edges which G does not. So if {u,v} is an edge of G, then it is not an edge in G^, and if there is no edge between vertices u and v in G, then an edge exists between them in the complement.)
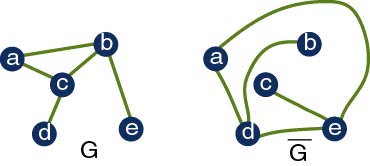
Claim: An independent set in G is a clique in G^.
Proof: If V' is an IS in G, then for all u,v in V', {u,v} is not an edge
(by definition of IS). This is true iff {u,v} is an edge in G^ for all
u,v in V' (by definition of G^). This is true iff V' is a clique in G^
(by definition of a clique).
This reduction is polynomial, since we are just taking the complement of a
graph.
Now we look at the degrees of the graphs involved. Note that we are looking at restricted sets of graphs for clique. We know that CLIQUE is NP-hard for general (as shown in class). What we want to show here is that it is also NP-hard for a restricted set of graphs (i.e. a subset of all graphs). In this case, we want to show that CLIQUE is NP-hard for graphs where deg(v) >= |V|/2 for all v in V (graphs whose vertices all have degree |V|/2 or more).
For the IS problem, we have the restriction on vertex degree that deg(v) <= 3. This means that in the complement graph G^, we will have deg(v) >= |V| - 4. (Think about it. The degree of a vertex v in G and its degree in G^ must add up to |V|-1, since an edge to any vertex u != v will exist in either G or G^.) So the above polynomial time reduction shows that CLIQUE for graphs with deg(v) >= |V|-4 is NP-hard, since we are given that IS (with deg(v) <= 3) is NP-complete.
For |V| >= 8, we have that |V|-4 >= |V|/2. We will consider only graphs that have 8 or more vertices. (For graphs with less than 8 vertices, chances are you can solve the problem by eyeballing it for a few seconds.) This means that any graph that has deg(v) >= |V|-4 will also have deg(v) >= |V|/2 (for graphs with |V|>=8), i.e. the set of graphs with deg(v) >= |V|-4 is a subset of the set of graphs with deg(v) >= |V|/2. So we can say that CLIQUE for graphs with deg(v) >= |V|-4 is a subproblem of CLIQUE for graphs with deg(v) >= |V|/2. We will call the former problem CL[V-4] and the latter problem CL[V/2].
Note that if we show that a subproblem B of a problem A is hard, then A must be hard also. (This is essentially what a polynomial time reduction from one problem to another does. But I won't try to explain that here.) This makes sense. If we know that we can't solve one part of a problem easily, then we know that we can't solve the entire problem easily either.
Since CL[V-4] is a subproblem of CL[V/2], and CL[V-4] is NP-hard by the reduction given above, we must have that CL[V/2] is NP-hard also. QED.
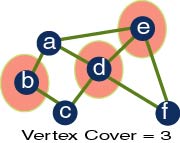
4) Apply the algorithm ApproxVertexCover to the following graph. Apply
VC to the same graph to determine if there is a vertex cover of size 2. Draw
the whole decision tree for VC, just like I did in lectures.
This is one of those do on your own questions. Applying the approximation
algorithm is very straightforward. Explain to yourself why the approx alg
returns a solution within 2 of optimal. For VC, simply do a brute force
algorithm - look at every subset of vertices of size 2 and check if the
subset covers all the edges in the graph.