308-360 Tutorial #3
General Dijkstra Information
Dijkstra╣s algorithm solves the single-source shortest-paths problem on a weighted, directed graph (digraph) G = (V, E) for the case in which all edge weights are nonnegative. Dijkstra╣s algorithm works by determining the shortest path weights from sink to vertex v. The shortest path weight of v, from s to v is d( s, v ). Note that d( s, v ) is not the length of the path, but the sum of the weights of edges along the shortest path.

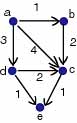
So, paths p1=< a, b, c, e > and p2=< a, d, c, e > are both length 4 and but the weight of p1 = w( a, b ) + w( b, c ) + w( c, e ) = 1 + 2 + 1 = 4 and weight of p2 = w( a, d ) + w( d, c ) + w( c, e ) = 3 + 2 + 1 = 5.
Just like in shortest common subsequence and other dynamic programming algorithms, the shortest path < s, v1, v2, ... , vk-1, v > contains a shortest weight path from s to vk-1, so d(s, v ) = d( s, vk-1 ) + w( vk-1, v ). So, build shortest weight paths by extending smaller shortest weight paths.
example: Find d( a, c ). Look at all shortest weight paths from a to vertices with an arc to c. Vertices a, b and d have an arc to c. d( a, a ) = 0, d( a, b ) = 1 and d( a, d ) = 3. d( a, c ) = minimum( d( a, a ) + w( a, c ), d( a, b ) + w( b, c ), d( a, d ) + w( d, c ) = minimum( 4, 3, 5 ) = 3. The minimum weight path from a to c, d( a, c ) = 3 and d( a, c ) = d( a, b ) + w( b, c ). Note that the minimum length path from a to c is < a, c > with length 1.
Tutorial Question 1
1. How can Dijsktra's algorithm be modified to give a shortest path tree
(equivalent to the breadth first tree)?
The values of the shortest weight paths returned by Dijsktra╣s algorithm are the sum of the weights of the edges along the path. If each edge were weighted with 1, then the shortest weight path would be adding 1 to the total weight from each edge of the path, which is equal to 1 x length of path. So, the shortest weight path from s to v when all weights are zero will be the shortest length path from s to v.
Modification to Dijkstra╣s algorithm as shown on slide 4 of Notes8 is to line 8.
original 8: d[s, v] = min{ d[s, v], d[s, u] + w(u, v)}
modified 8: d[s, v] = min{ d[s, v], d[s, u] + 1}
To return a shortest path tree, it is necessary to calculate the parent vertex of every vertex. Initialize pi(v) = null for all v in V. Every time the value of d[s, v] is updated with d[s, u] + w(u, v), set pi(v) = u. Vertex u is therefore the k-1th vertex of the k length shortest weight path from s to v.
Dijkstra╣s algorithm is like BFS in that set S corresponds to the set of black vertices in a BFS because black vertices in BFS have their correct breadth-first distances and vertices in S have their final shortest-path weights.
Tutorial Question 2
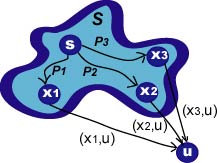
2. Apply Dijkstra's algorithm to digraph pictured in the tutorial. Identify the edges
in the shortest paths tree. S is the set containing all vertices whose shortest weigh path has already been determined.
Stepping through Dijkstra for G = ( V, E ). Each vertex v in V has a shortest weight path value d[s, v].
1. Set d[s, v] = infinity, and d[s, s] = 0.
2. Let Q = V, and now do the following until Q is empty.
3. u = minimal d[s, v] for all v in Q.
4. For each vertex v adjacent to u ( i.e. for each vertex u points to ), set d[s, v] = min{ d[s, v], d[s, u] + w(u, v)}
5. Add vertex u to S.
5. Remove vertex u from Q because we have found its shortest weight path.
To understand this, make a table:
vertex | d( s, v ) | membership | adj( v ) |
Vertex v╣s membership identifies if v╣s minimum weight path has been determined with respect to the entire graph. For the alg, this would be in Q or not in Q. Simply fill in the table as you step through the algorithm. It is useful to make a table for each iteration and then examine the changes in the table values from one iteration to the next.
Tutorial Question 3
3. Apply Bellman-Ford's algorithm to the following digraph. At each pass
through the main loop, record the value d[s, u] computed for each vertex.
The Bellman-Ford algorithms solves the single-source shortext-paths problem in the more general case in which edge weihts can be negative. As with question 2, create a table for each iteration and fill in the elements of the tables. Verify that the last iteration╣s table contains the correct answer.
Dijkstra:
2. Let Q = V, and now do the following until Q is empty. ( for all vertices of V )
3. u = minimal d[s, v] for all v in Q.
4. For each vertex v adjacent to u ( i.e. for each vertex u points to: ( u, v ) ), set d[s, v] = min{ d[s, v], d[s, u] + w(u, v)}
BellmanFord ( corresponding lines number as in Dijkstra )
2. For |V| - 1 vertices do the following ( for all but one vertices of V )
3. { is not in BellmanFord }
4. For each vertex v adjacent to each vertex u ( i.e. for each vertex u points to: ( u, v ) ), set d[s, v] = min{ d[s, v], d[s, u] + w(u, v)}
Tutorial Question 4
4. Construct a digraph without negative weight cycles for which Dijkstra's
algorithm does not work.
CHANGED!!!!
Dijkstra╣s algorithm produces incorrect answers for a directed graph with negative-weight edges. this is shown is the proof of Theorem 25.10 in Cormen. The contradiction in this proof relies on the fact that d( s, y ) <= d( s, u ) when path p from s to u can be decomposed as
< p( s to x ), ( x, y ), p( y to u ). Note that s and x are in S, and s can equal x, and y and u are in V-S and y can equal u. Since all d( s, v ) are positive, because all weights are non negative, d( s, y ) <= d( s, u ) and therefore d[y] <= d[u]. When the graph has negative weights, this inequality no longer holds ( d[y] could be > d[u] if the weight of p( y to u ) is negative ).
Intuitively, let d[v] be a finalized shortest weight path from s to v and let u not be a member of S at that iteration. Then we know that d[v] does not include a path from s to u. In a following iteration, d[u] is finalized. If ( u, v ) exists and d[u] + w( u, v ) < d[v] then contradiction because there is a d( s, v ) < d[v].
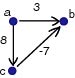
Here is what Dijkstra does: It finalizes d(a,a)=0, then in the next iteration
finalizes d(a,b)=3. Then in the next iteration finalizes d(a,c)=8. Dijkstra
does not check the (c,b) edge because it does not update d(s,b) since d(s,b)
has already been finalized.
Tutorial Question 5
5. Use Prim's algorithm to find a minimum spanning tree in the following
graph (see tutorial).
Prim╣s algorithm is a special case of the generic minimum-spanning-tree algorithm. Prim╣s algorithm has the property that the edges of the set A always form a single tree.
MST-Prim( G = (V, E), w, r )
- key field specifies the vertices not in tree priority in Q.
1. Q = V
2. for each u in Q do key[u] = infinity // no edge connecting u to the tree
3. key[r] = 0
4. pi[r] = nil
5. while Q not empty do
6. u = EXTRACT_MIN( Q )
7. for each v in Adj(u), (u,v) do
8. if v in Q and w(u,v) < key(v) then
9. pi[v] = u
10. key[v] = w(u,v)
- key[v] is the minimum weight of any edge connecting v to a vertex in the tree.
- pi[v] is parent of v in the tree.
CLR Excercise 25.2-1
25.2-1
Run Dijkstra╣s algorithm on the directed graph of figure 25.2 (Cormen), first using vertex s as the source and then using vertex y as the source. In the style of Figure 25.5, show the d and pi ( parent ) values and the vertices in set S after each iteration of the while loop.
Follow the same method as detailed in tutorial question 2, but add a parent field to the table. The parent field is equal to vertex u when d( s, v ) path = < s, v1, v2,... u, v > or is equal to null if the path = < s, v >. To do this in the same form as Figure 25.5, simply write the table values in their appropriate locations on the graph.
CLR Excercise 25.2-3
25.2-3 Suppose we change line 4 of Dijkstra╣s algorithm to the following.
4: while |Q| > 1
This change cause the while loop to execute |V| - 1 times instead of |V| times. Is this proposed algorithm correct?
Yes. Consider the following figure. At each iteration, one vertex is added to S. So, after |V| - 1 iterations, |S| = |V| - 1. Let u be the one vertex not in S. Let x be any vertex to which u is adjacent to. A shortest weight path from s to u can be decomposed into a path from s to x and an edge from x to u. Note that x could be s, and therefore the path from s to u would be the edge from s to u. All paths from s to x are contained within S, because for the d[x] to be finalized, it must be based on other finalized d[v]╣s. At the last iteration, the predicted d( s, u ) is the minimum weight of all possible paths s to u. Because d[v] has been finalized for all vertices v except u, the predicted value is the final value. There is no non-finalized d[v] that could contribute to a lower d( s, u ) than the d( s, u ) predicted at the |V| - 1th iteration. So, d( s, u ) at the |V| - 1ith iteration is in fact the final d( s, u ). The only thing to remember, is not to use S as the set of all vertices with d(v), must use V, otherwise would not include vertex u.